Appeal for a higher power
Grant me the strength to accept that I cannot change the p-value, the power to distinguish between absence of evidence and evidence of absence and the wisdom to know the difference.
Imagine you are looking at a screen – much like you are doing now. On this screen are moving dots and you count how often they collide with each other. While you are doing that – unbeknownst to you – an unexpected moving square is entering the screen from the right and moves until it exits on the left side of the screen. Would you be surprised to learn that the *less* time the square is visible on the screen, the *more* likely you would be to notice it? Most people would – understandably – find that quite surprising. And yet, that is what is happening. As this might sound a bit counterintuitive, we have to go on a bit of a detour to fully understand it. So please bear with us, we promise it is all relevant.
For the first two years of WW2, the US Navy did not possess a functional torpedo. This sounds like an incredible claim, given that the war in the Pacific made especially strong use of such weapons. The reason for this is that the Empire of Japan relied heavily on long supply lines throughout the Pacific rim (as the Japanese home islands are resource poor) rendering them particularly vulnerable to submarine attack. In theory, the US Navy possessed a very advanced weapons system – the Mark 14 torpedo – to get the job done. This torpedo featured several key innovations, one of them being that instead of detonating when colliding with the – often armored – side of the target ship, like conventional torpedoes (which usually requires multiple hits to sink a ship) it would run underneath it, when the steel of the ship would trigger the magnetic proximity fuse of the torpedo, setting off an explosion from directly underneath that would break the back of the ship and sink it with a single torpedo.
So far the theory. And yet, between December 1941 and November 1943, over ⅔ of Mark 14 torpedoes fired in anger failed to detonate, most of them running harmlessly beneath the Japanese ships. How is this possible and what does this have to do with cognitive psychology?
The principal reason for the failure of Mark 14 torpedoes to detonate consists in the fact that they were running too deep, which did not trigger the magnetic proximity fuse as the torpedo was in fact much too far, and not proximate to the hull. The Mark 14 torpedo had a depth control mechanism that was designed to maintain a set depth below the surface which relied on a calibrated hydrostatic gyroscope system. This system was also state of the art for the time. So what was the problem and how could it persist for so long?
The crux of the problem is that when the torpedo is moving, cavitation creates turbulence, lowering the water pressure at the sensor locally, which will make the hydrostatic system that controls its depth believe that it is running too shallow, which will make the torpedo dive deeper in order to adjust. So far the key problem. The reason why it was not discovered for so long was that at first – incredibly – only static torpedos were tested, as this made retrieval easier, and the static torpedoes could maintain any desired depth that was set by the operators. Only when submariners frustrated by far too many duds insisted on realistic live firing exercises were they finally performed. Once the problem was identified and fixed, the US silent service had a very effective weapon in the form of the Mark 14, using it to devastating effect in 1944 and 1945.
There were several other testing-related issues involving the Mark 14 as well, but the key take home message here is that it does matter a great deal under which conditions a system is tested, and whether these conditions are realistic or not. If they are not, even severe problems could remain undetected.
This issue is not restricted to torpedoes or war. If an alien civilization found a piston-engine aircraft in a hangar and only tested it inside of it, aircraft would be very puzzling contraptions, and their true purpose would not be immediately obvious. Proper context matters.
Psychology often suffers from a similar problem. Many times, phenomena that appear to be devastating biases and deficits – for instance the “baserate fallacy” – disappear when investigated under more ecologically valid conditions. For instance, it can be shown that if doctors are presented with information about the accuracy of medical tests in terms of the probabilities that the test results will be false positives or false negatives, they are systematically unable to do so. Specifically, they overestimate the probability that a patient with a positive test result actually has the condition, if the medical condition is rare. This has been interpreted as “baserate neglect”, the inability of most doctors to take the low baserate into account when making their calculations. This is puzzling, as the doctors are certainly smart enough to do so, but they empirically don’t.
However, it can also be shown that if the very same doctors are presented with the exact same information in terms of natural frequencies instead of probabilities, doctors can reason about this problem just fine and come up with the correct answer, without exhibiting baserate neglect. Apparently, these doctors are able to handle this information just fine, if they encounter it in the format that brains would have encountered it most of evolution: relative counts. In contrast, as the concept of probability is a relatively recent cultural invention that is only a few hundred years old, one would not expect brains to be particularly comfortable with probabilistic information.
To summarize – what can appear as a cognitive deficit or an impairment of reasoning – baserate neglect – disappears, when tested under conditions humans would have encountered for most of their evolutionary history.
This state of affairs seems to also be true for other cognitive domains, such as attention.
Inattentional blindness is the failure of an observer to notice unexpected but readily perceivable stimuli when they are focusing on some task. This phenomenon has been documented in many contexts, even including unexpected stimuli that are moving. It is commonly explained in terms of the overriding strength of top-down goals and expectations over bottom-up signals and often seen as an inescapable flip side of focusing attention. In other words, the benefit an observer gets from deploying attentional resources to task-relevant stimuli is paid in form of an increased likelihood of missing less relevant stimuli.
Importantly, this phenomenon is often interpreted as a deficit, as it manifests as a pervasive failure of observers to notice unexpected objects and events in more and less serious real world settings, from the failure of experts to notice a gorilla embedded in radiographs to the failure to notice Barack Obama to the failure to notice brawls while on a run, the latter which could have implications for the veracity of eyewitness accounts and on and on.
Some even went so far as to suggest that inattentional blindness might be an inescapable cognitive universal, insofar as it has been documented in every culture it has been tested.
Given how prevalent and – indeed inescapable and deleterious – the phenomenon of inattentional blindness seems to be, it struck us that it would leave organisms in an extremely vulnerable state.
As we are all the offspring of an unbroken chain of organisms who all successfully managed to meet the key evolutionary challenge of reproduction before disintegration, this seems implausible.
It could be argued that the real cognitive task all organisms are engaged in is the management of uncertainty. Specifically, an organism does not a priori know which stimulus type in the environment is most relevant. Of course, there are some potential stimuli that are either expected or consistent with goals, but that does not mean that unexpectedly appearing threats might not suddenly be more relevant. Thus, it would be unwise if an organism overcommitted to focusing attention solely on those it deemed relevant at the time it decided to focus. In other words, there should be a path for evolutionarily relevant stimuli to override top-down attention.
Fast motion is an ideal such stimulus, for several reasons. First, most organisms devote a tremendous amount of cortical real estate to the processing of visual motion. Second, motion is generally a fairly good life-form detector. Third, fast objects are particularly likely to be associated with threats like (close) predators. Fourth, fast moving stimuli are relatively rare in the environment, which makes false positives less likely.
We could not fail to notice that in spite of the many variations of inattentional blindness experiments performed in the past 3 decades, no one had tried to measure the impact of fast motion on inattentional blindness, not even those who had created experimental setups that made the parametric variation of speed straightforward. In fact, the only studies that – to our knowledge – varied speed systematically at all tried slow and slower speed conditions (relative to background motion), concluding that duration on screen – not speed – matters for the detectability of unexpected objects. Thus, to our knowledge, the attention system had never been explored under conditions of fast motion, a very plausible and – in evolutionary terms – important stimulus.
So we did. Briefly, we used a high powered sample of research participants in 3 studies that included conditions where the unexpected moving object (UMO) was fast, relative to background motion. The first experiment was a replication of the original “Gorilla” study. The second experiment involved detecting an unexpected moving triangle when counting dots passing a vertical line and the third experiment replicated this, while also including conditions that featured triangles that were moving slower than the dots.
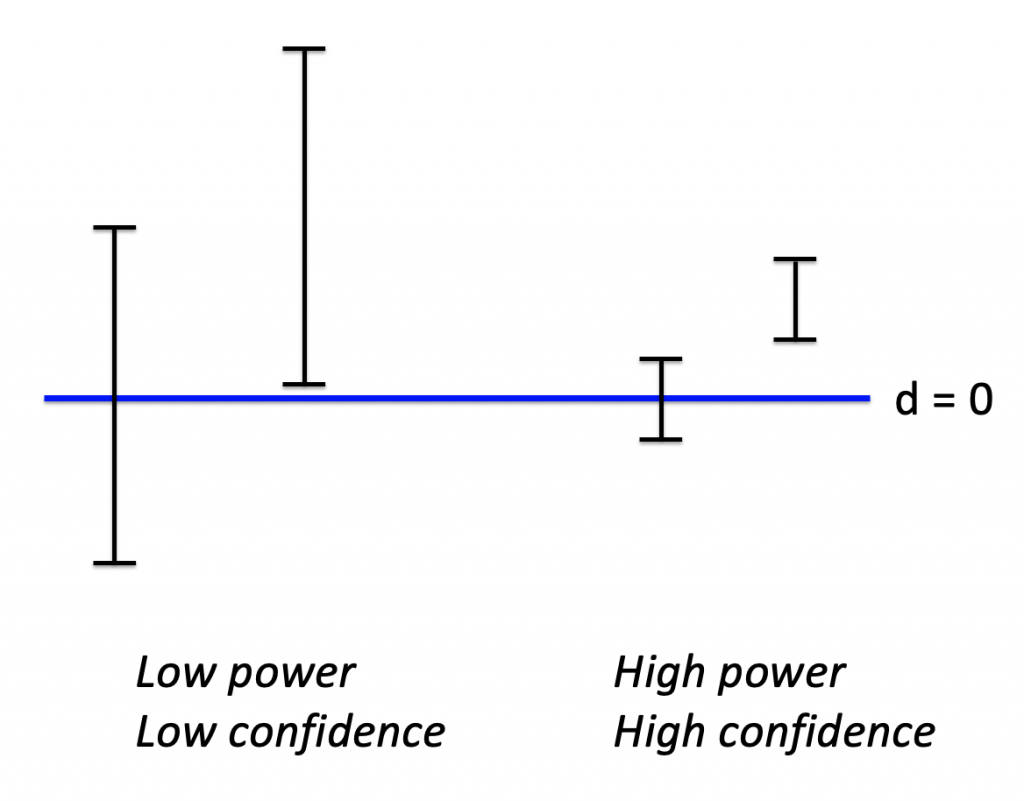
The results from these experiments are clear and consistent. Faster moving unexpected objects are significantly more likely to be noticed, implying diminished inattentional blindness. Importantly, this effect is asymmetric. Even though the UMOs are on the screen much longer when moving slower than the dots, remarkably the faster moving UMOs are much more noticeable. This rules out that mere physical salience (the contrast between stimulus features) is driving this effect – if it was, slower moving UMOs should be as noticeable as fast ones. But this is not the case.
In other words, far from being a deficit that somehow diminishes cognition – in the same way cognitive biases have been suggested to do – “inattentional blindness” might be ironically named, as it highlights the elegance and sophistication of attentional deployment.
As we mentioned, an organism does not know ahead of time what will be the most relevant stimulus at any given time, under conditions of uncertainty. In the real world, uncertainty is unavoidable, so it has to be managed. Put differently, it would behoove an organism to hedge their attentional bets before going all in on one goal. Fast motion is a reasonable evolutionary bet to signify highly relevant stimuli – be they predator or prey – that an organism should be apprised of, whether they expected them or not. And it is precisely with fast motion that we get – to our knowledge for the first time – demonstrably strong attenuation of inattentional blindness.
Thus, rebalancing top-down goal-focused attention with relevant bottom up signals such as fast motion allows an organism to eat its proverbial cognitive cheesecake (by focusing attentional resources on what matters as defined by an important task) and “have it” too, by allowing for fast motion to override this focus, thus hedging for potential unexpected real life threats.
On a deeper level, big data management principles suggest that it is critical to filter large amounts of information up front. As perceptual systems are in this situation – having to handle high volumes of information, it is plausible that a key task is to reduce the information, ideally by filtering by relevance for the organism. In this view, “inattentional blindness” is simply one way in which this filtering by relevance manifests. So this view is incomplete, as it only captures the part of filtering by relevance that is due to top-down, goal-dependent relevance. Other ways in which stimuli might be relevant is due to expectations or inherently relevance, like fast motion.
So, when tested under the right conditions, people behave smarter than commonly believed.
This post consists of two parts. The first part is aimed at introducing this new illusion to a general audience. The second part is intended to supplement technical details for specialist readers. Click here to navigate to the technical section of this post
Most people believe that what they see corresponds to reality, a philosophical position called “naive realism“.
This position is challenged by the existence of visual illusions, where perception differs from reality, revealing the subjective nature of our perception.
One such class of visual illusions is known as “illusory contours”. Presented with this illusion, observers perceive edges that are not actually there. The most well-known example of this phenomenon is the “Kanizsa triangle”.
Most observers interpret this scene – assuming one is looking down from above – as a white triangle being on top of three black circles as well as another triangle, not as three pac-men and < ^ > symbols that just randomly happen to align in this configuration just by chance.
This illustrates another interesting principle of perception – there is compelling evidence that the brain favors the most likely (often the simplest) interpretation of a scene. In other words, the brain is routinely “connecting the dots” to fill in information that is not actually there, and has to do so, as not all necessary information is always fully available. These “best guesses” are often accurate, aiding in the survival of the organism.
All of this has been known for many decades.
In the image at the beginning of this post, bright – but fleeting – rays appear to emanate from the center of the image, akin to seeing the sun breaking through the clouds. Thus, we call this effect the “Scintillating Starburst“. However, these shimmering rays are entirely illusory: they’re the result of our brain connecting the dots. The starburst is not physically present.
What distinguishes this illusion from known effects is that in the Kanizsa triangle, the inducers (the pac-men) are luminance defined, whereas in our Scintillating Starburst, they are themselves the result of subtle features of our visual system.
Without getting too technical here (for details, see our paper), the Scintillating Starburst illusion can be explained as such: The black concentric “wreaths” (technically pairs of scaled star polygons) are all uniformly colored, but the part of our visual system that processes information from the periphery sees the intersection points as brighter than the rest of the wreath. As these “beacons” of brightness are aligned in linear fashion (along a ray projecting from the center), we believe the brain is connecting the dots accordingly, which is why most people see these illusory rays. What makes them shimmer or scintillate is the fact that another part of the visual system (that which processes information at the center of gaze) does not see the intersection points as brighter, but rather as they actually are. Thus, these rays will be fleeting due to the dynamic interplay between these two systems.
The phenomenology of this effect can be quite striking, and further enhanced by optimizing all stimulus dimensions (see paper) and by rotational motion.
Thus, the Scintillating Starburst is perhaps best understood as a “compound illusion” combining – and revealing – several features of our visual system, much like the “Lilac chaser”.
People readily interpret their environment in light of incomplete or unreliable information. For instance, when looking at stars, some observers are prone to see constellations. We believe the tendency of some people to “connect the dots” is related to their propensity to see non-existing ray patterns, for the same reason.
Note: This illusion was a finalist in the 2020 “best illusion of the year” contest.
The purpose of this second part of the post is to address several technical points that did not make it into the paper itself (mostly because this was not the focus of the article, the reviewers asked us to take it out or it would have been too much of a tangent). Nevertheless, these points are important, so here we go.
First – and perhaps most importantly – we would like to emphasize that – contrary to popular belief – this is not a grid illusion. Most superficially similar effects and phenomena such as the scintillating grid, the Hermann grid, the Motokawa grid or the pincushion illusion are confined to grids, even radial versions of these grids. The Scintillating Starburst is going off the grid. Nor are we convinced that the underlying mechanism is the same or even similar. The phenomenology of the Starburst seems to be qualitatively different – the rays are stronger and more striking and at the same time fleeting or scintillating, traversing the background. In other words the rays are not bound to a grid.
However, it is worth noting that this illusion is perhaps best conceived of as a compound illusion, much like the Lilac chaser (which combines the phi phenomenon, afterimages and Troxler fading). Here, single, short segments of Motokowa-grid lines are perceived within each wreath. These short “Motokowa line segments” plausibly serve as guides or gestalt cues for the perception of occluding lines that traverse the background. However, the segments covering the wide distance between the wreaths are qualitatively different. This is consistent with the fact that there is a “Gestalt” tendency to extrapolate illusory contours. The final part of the compound illusion consists in the fleeting nature of the rays, which appear and disappear following saccadic eye movements. We attribute this to a competition between foveal and peripheral vision. Foveal vision has the resolution to discern that there are no Motokawa-style lines present, whereas peripheral vision does not, and this interplay causes the dynamic nature of the illusion, in synch with eye movements. This explains why 1) the strongest rays appear in the periphery. 2) why the rays shimmer as a function of saccadic eye movements. 3) why the Motokawa segments are more persistent than the entire illusory ray when fixated upon. 4) Why the illusory rays vanish upon fixation. 5) why the rays appear phenomenologically different than other grid illusions — the tiny grid illusions act as illusory guideposts for the illusory rays.
Oddly, the Fourier transform (FT) of the Scintillating Starburst stimulus closely corresponds to the illusory percept. To our knowledge, this is essentially unique to this stimulus class. However, we are aware that – curiously – the FT is neither necessary nor sufficient to predict the appearance of all Scintillating Starbursts. Specifically, the match is perfect for Starbursts that are made up of Star Polygons with a base that is odd and a denominator that is even, such as 14/2 (in Schläfli notation) as well as for Star Polygons with an even sided base and an odd denominator, such as 18/3, but Starbursts that are made up of Star Polygons of the other possible combinations, 21/3 or 28/4 would be phase-shifted by a set fraction of the vertex angle of the base polygon, e.g. a 12/2 would be phase-shifted by a quarter of the vertex angle of the hexagon or 15 degrees. We realize this is a bit abstract, so see the figure below for illustration.
This peculiar behavior is likely due to the fact that only half the odd-n/2 starburst is needed to get the ray pattern in the FFT — this is *probably* a consequence of the fact that even-sided polygons have faces that are opposite each other and thus “cancel out”. When making star polygons with even-sided base polygons the angles get rotated such that rays no longer cancel as before and the number of FFT rays then corresponds to the number of illusory rays in the full starburst. Unlike odd-sided polygons with faces opposite vertices, these thus don’t cancel out. Again: Only half the starburst is needed to get the FFT rays to match the full stimulus, as the FFT is symmetric.
Another consideration is the issue of “higher order” Starbursts (that are made up of star polygons with Schläfli numbers larger than the ones used in our study). For instance, Starbursts made up of bisecting star polygons (e.g. 14/2) are just a special case. n/3 starbursts trisect each other and still yield Scintillating Starbursts. Of course, such considerations open up a vast stimulus space. We are not claiming we found the most optimally possible Starburst (the one that evokes the strongest rays overall). The 14/2 Starburst is just the one we came across – serendipitously – first, so that is what we focused on in our empirical study.
This brings us to another consideration worth noting. To fully appreciate it, we first need to introduce some necessary terminology: A “wreath” consists of scaled pairs of Star Polygons such that they overlap. An “optimized wreath” consists of *scaled pairs* of Star Polygons that have minimal overlap. This is important because each Starburst has an optimal scale factor such that the star polygons just touch. When constructing Starbursts, one can either keep the scale factor and spacing between wreaths constant or vary it for each kind of star polygon. We decided to keep these factors constant (arguably a reasonable choice, given the vast potential space of stimulus dimensions), effectively optimizing all stimuli in our study to the 14/2 starburst, which is part of the reason why the 14/2 Starburst was perceived to evoke the strongest rays. It is possible that optimized 12/2 or 10/2 Starbursts could evoke rays with a similar strength as a 14/2, just fewer of them. Note that this consideration does not change any of our interpretations and conclusions of the paper. The point of this paper was to introduce the illusion and determine which – and how much – low-level visual attributes (such as contrast) contribute to the effect. Now that this has been determined, fully optimized starbursts can be explored properly.
This bring us to the final point of this section, future directions. Four such directions seem obvious. One of them is – as mentioned – to determine which Starburst truly evokes the strongest effect – which is now feasible (doing this at the same time as the exploration of the low level features would have led to a combinatorial explosion, as the stimulus space is too large). See figure below for an appreciation of just how large this stimulus space is.
Second, we used subjective ratings as a dependent variable. Comparative judgment (2AFC) might be a better way to explore this effect psychophysically going forward, perhaps in conjunction with probing the underlying neurophysiology, which is the third point (our suggested mechanism – the dynamic interplay between foveal and peripheral vision is admittedly speculative at this point). Fourth – and finally – it would be interesting to link the propensity to see rays in the first place to personality characteristics. Not everyone sees constellations in the sky, just individual stars. Others cannot not see the constellations. It seems self-evident that there might be a differential propensity to connect the dots.
Finally, we would like to note an interesting observation which strengthens the conclusions we present here and in the paper. If the background is brighter than the shape, the illusory rays will appear brighter than the background. If the background is darker than the shape, the illusory rays will appear darker than the background. If background and shape are isoluminant, no rays appear (see figure below).
Note that nowhere in this account did we mention color. This seems to be strictly a story about luminance, not chromaticity. In other words, the mechanism we proposed above (and in the paper) is likely to be true – if there are “beacons”, rays emerge. If there are no beacons, there are no rays. The rays themselves are bright or dark, not colored. Taken together, we take this to suggest that our account – the interplay between the magnocellular system which creates the perception of the rays and the parvocellular system which doesn’t see them is likely to be correct.
To get a striking experience of how this is the case for a wide variety of color combinations and corresponding ray strengths, have a look at this video.
This brings us to a final point, namely similarity and differences to other, known effects. We have covered much of these already in the introduction to our paper, but this observation re color above (in addition to the considerations re Fourier Transform and luminance defined streaks we discuss in the paper) provides further evidence that we are dealing with a distinct phenomenon here:
As noted above, Scintillating Starbursts of any color yield either rays that are darker than the background, brighter than the background, or no rays. They do not yield colored rays. In contrast, the pincushion illusion does. Here, we made radial versions of the pincushion grids featured here. The illusory color is quite striking and clearly evident.
These color effects are undeniable. Moreover, these illusory lines or rays entirely static. They are not fleeting or scintillating. As Starbursts do not produce colored rays, but rays that scintillate, these are evidently different phenomena.
Finally, we would like to note that the effect of induced scintillating rays is maximized if the line width of the wreaths that make up the Starburst stimulus scale with cortical magnification. Cortical magnification means that more real estate in the visual cortex is dedicated to central vision than to peripheral vision. So to make stimuli equally visible, they have to be scaled up, if they are presented in the periphery.
Existence has long been associated with the pain of living. Everyday life inherently poses many challenges to physical and mental integrity. Modern life in particular is characterized by frequent assaults on self-esteem in the form of unceasing comparisons to others via social media, popular culture and advertising. These inadvertent challenges to the self trigger insecurities in many people. Some of them cope with the associated mental pain by performative self-elevation (or “flexing”). Examples of flexing include casual name-dropping, boasting about one’s material or moral self-worth, or pretending to be part of the cultural elite. Of course, some people always had such tendencies, but it is telling that Gen-Z coined a term for this phenomenon (akin to Germans having a word for “Schadenfreude” – people from all cultures recognize the emotion of deriving joy from someone else’s misfortune, but Germans actually have a word for it).
Our research identified the people who are particularly prone to engage in this flexing behavior. It is – in principle – possible that people with such tendencies are genuinely grandiose. However, our findings suggest that this is not the case. Conversely, it is – in particular – highly insecure individuals who tend to do most of the flexing. We also found a strong relationship between insecurity and narcissism (the correlation is astonishingly high, at the limits of what one could expect, given the underlying reliabilities of the instruments used to measure these constructs). This suggests that narcissism (“extreme self-love”) might be widely misunderstood. Instead of being characterized by excessive self-love, the exact opposite seems to be the case. Narcissists appear to harbor deep-seated insecurities and – if triggered by challenges to self-worth – they tend to cope by flexing.
Of course this research raises several important questions. For instance, it would be interesting to know how challenges to self-worth, insecurity, narcissism and flexing interact and develop in the long term. One peculiar consequence of flexing behavior is that it does not actually elevate the individual socially. In many cases, it will instead have a paradoxical effect: As some consider narcissistic behaviors to be particularly annoying, exhibiting them adds to their experienced pain of living, which in turn makes them like the flexing individual less. In other words, while flexing represents a short-term band-aid to one’s injured self-esteem, it makes others who consider flexing to be insufferable think even less of them in the long run, particularly if the flexing is cringe.
From this perspective, narcissism is the end-result of a runaway maladaptive cascade – a vicious cycle between social challenges to self-esteem and ill-advised coping mechanisms (flexing) – which reinforce each other over time. Whether this is actually true will have to be the subject of future research. It is also unclear why not everyone responds to social comparison with flexing. There might be other predisposing factors that have to be jointly present (perhaps lack of self-awareness or social skills) that bring about this unpleasant behavior in some individuals.
Our study also highlights the notion that behavior cannot be taken at face value. Motivations matter. For instance, psychopaths – who tend to be genuinely grandiose – might exhibit the same behaviors as narcissists, but for very different reasons. It is possible to tease these apart, i.e. one could conceive of a study showing that narcissists seek status whereas psychopaths seek power, but by using behaviors that are similar on the surface-level.
Three final brief points:
To conclude, the tidal wave of narcissism, flexing and insecurities can perhaps be chalked up as another unintended consequence of modern information technology, along with the amplification of hyper-polarization. In the long term, society will have to come to terms with these developments if it is to avoid total collapse.
People could be forgiven for initially believing that COVID19 is just like the flu, as many have personal experience with the flu and gotten used to the risk posed by the flu.
This tendency towards complacency was reinforced by bad takes in the media or from academia along the lines of “the real risk is hysteria”.
To be fair: Panicking is rarely helpful and it is important to put potential risks into perspective.
The flu is indeed serious, but we have a good idea of just how serious it is likely to be. This is due to the fact that it is happening every year and that we have been observing the seasonal flu for a long time, so there is plenty of data.
Here, we graphed the annual mortality attributed to the flu in the United States for the past 40 years, as reported by the CDC. We have data going beyond that time period, but it is hard to integrate, as reporting criteria have changed, and it is not easy to estimate how many people actually die from the flu, as a large proportion die from secondary pneumonia, not influenza per se. So for an apples to apples comparison, we keep it at this.
This graph is a frequency histogram. Black bars represent how often a flu season led to a given number of deaths. For instance, twice in the past 40 years, flu claimed less than 5000 people a year (the left-most bar). As you can see, the distribution of mortality due to the seasonal flu is roughly normal – albeit with a slight skew. The expected death rate from a given seasonal flu is captured by the blue line, which represents the median, at about 25,000 cases. Importantly, how deadly any flu season can be expected to be clusters in a narrow range around this central value. There was only a single flu season in the last 40 years with more than 60k deaths, in 2017/18. A few times, the flu season was mild, such as in 1986/7 and 1978/9, with 3,349 and 4,681 cases, respectively.
In other words, we more or less know what to expect from the seasonal flu – the range of typical outcomes is rather narrow within about one order of magnitude, and while 25k cases is a serious toll for the United States as a whole (about 2/3 as many as people who die in car accidents per year), the individual annual risk is low, at around 1 in 14,000.
The coronavirus – which leads to COVID19 is not like that, because it is new, so we do not know how the mortality from COVID19 distributes, yet. Early reports indicate that it is highly contagious (every person who has it seems to infect 2.5 others, compared with about 1.3 for the seasonal flu) and mortality seems to be high, with between a 2% and 3% of the people who test positive die from the disease, on average.
The very fact that these numbers are very much in doubt – mortality estimates in the literature vary widely, depending on how many cases are tested – reflects how much uncertainty there is about COVID19, at this point.
Let’s assume that people treat it just like the common flu and don’t implement serious social distancing or containment measures. In that case, we can expect that 50% of the US population will eventually get this virus and 1% will die from it (these estimates are extremely conservative, as experts believe that up to 80% of the population could get infected in this case, and that the mortality could be up to 3.5%).
In that case, we could expect close to 2 million fatalities from COVID19 in the United States alone. This sounds dramatic, but is in line with the outcome of the last severe pandemic. To put this in the context of the seasonal flu, we now represent this estimate in the same graph as above, as a red line.
If the experience in Wuhan and Italy is any indication, the reason for this terrible death toll is mostly due to a local lack of ventilators, which leads a serious case of the illness to take a fatal turn.
The good news? It appears that this terrible outcome is entirely preventable. Containment (as in China), massive testing (as in South Korea) and early intervention (as in Taiwan and Singapore) seem to have curbed the devolvement of the situation into a million+ fatality scenario in each of these countries. It’s not entirely clear what the role of factors like temperature (particularly in Singapore) is, but it is highly encouraging that we can prevent a catastrophic outcome if we do take the disease seriously enough, early enough.
So let’s assume that we take decisive action (social distancing, hand washing – with soap, no face touching, lots of testing) and we get the same outcome as China, which is actually a pessimistic take, as our population is much smaller. That outcome is now represented in green – it would manifest as a bad flu. In other words, if we take such actions now, cases will likely mount for another month or so, but then peter out by mid-April.
Of course, reality is highly ironic. If there are no good options available, leaders will not get credit for taking the bad option that prevents a catastrophic outcome, as the counterfactual is not observable. Thus, it is particularly important to keep that in mind and act – decisively – as soon as possible.
Action potential: The virus has the potential to be catastrophic, but doesn’t have to be, if people do the right thing now.
Today, 5 years ago, “the dress” broke online, and we have come a long way since then. If nothing else, this is a scary reminder of how fast time passes while one is busy doing other things.
There were lots of clickbaity “explanations” of the phenomenon (like women having 4 cones) offered immediately, whereas others dismissed the phenomenon as being just another example of mass hysteria, the phenomenon, suggesting that there is nothing to see here, as this just reflects the impact of different screen settings.
Some (including us) realized that this is a completely novel phenomenon (displays like rubin’s vase or the duckrabbit are bistable within people, this is bistable *between* people, or within the population. Most people cannot switch the percept spontaneously). We also pointed out that we don’t know what is going on.
It took 2 years to establish that. Basically, it depends on what you believe about the illumination. And that depends on your experience. In cases where there is uncertainty about the illumination (as in this photo), these beliefs dominate the percept. As people have different experiences, they perceive different things: https://slate.com/technology/2017/04/heres-why-people-saw-the-dress-differently.html
After that, we realized that there are such phenomena for hearing (https://www.buzzfeednews.com/article/virginiahughes/yanny-laurel-audio-conspiracy-theory) and other visual stimuli (like the sneakers). The field also established other parameters that matter, i.e. the impact of pupil size on the individual percept, or how fast people change their mind.
What was left to do was to be able to *create* such a stimulus at will. It is most compelling to say that one understands the phenomenon when one can create it in a principled fashion. We have now done that as well: Using crocs, of all things.
Using crocs might sound – on the surface of it – even more ridiculous than the dress, but there is a deep principle (which we call SURFPAD) at work: Whenever you combine Substantial Uncertainty with Ramified or Forker Priors or Assumptions, you will get disagreement.
In the case of the crocs, this means to take an item (like crocs) that could be any color and put it on a black background to take away context cues. Then shine a complementary light on it to make it appear grey. But also include an item (such as the white socks) that will reflect the light. So objectively, there are grey crocs and green socks. But those who know from prior experience that the socks are actually white will mentally subtract that, and they perceive the original color of the crocs and white socks.
This is critical to understand our polarized times. To give an example from journalism: Say I wrote a piece on how someone is incompetent. But if you don’t know me or that person, you do not know whether that person is truly incompetent, or if I’m just being mean. Some people know that anyone can be put in a bad light, so if your prior belief is that the author is biased, the piece will be ineffective. Other people have a prior belief that the person is actually incompetent, so they will believe the author. Both kinds of people walk away feeling that their position has been confirmed by the ambiguous evidence, deepening the difference in priors, furthering the divide.
If you have a couple of minutes and want to help us get to the bottom of some of the more subtle aspects of sneakers, crocs and the like, you can click here to donate your data.
What color are these crocs?
*We are aware that lights don’t have colors. Notoriously, lights are not themselves colored, as the color experience is created in the brain. However, light – a form of electromagnetic radiation – has a frequency, which corresponds to a certain wavelength. Humans see lights in a relatively narrow wavelength range, typically between about 400 and 700 nm. Radiation with longer wavelengths (think a laser with 650 nm) is typically perceived as red, whereas one at 441 is perceived as blue. Generally, lights with longer wavelengths reddish, shorter blueish. Being aware of all that, we say “red light” as shorthand for light that contains power at predominantly long wavelengths, to make for a more concise text, much like neuroscientists say that neurons have “tuning preferences” (say for stimuli of a certain orientation or spatial frequency), being fully aware that people have preferences, neurons (lacking agency) do not. In other words, most neuroscientists say that neurons have preferences as a shorthand to make communication more efficient, they are not committing a mereological fallacy, as they are sometimes accused of by philosopher. The same applies here to our use of colored lights or pink shoes – the “pink shoe” is shorthand for a shoe that appears pink to most observers without visual impairments and under typical lighting conditions.
Pascal Wallisch & Michael Karlovich
The degree of polarized disagreement about current events is at an all-time high, and rising.
So we need to understand disagreement better in order to avoid disagreeable results.
A key problem when studying discord in politics or economics is that all issues are loaded – people have entrenched positions that might make it hard for them to accept some potential conclusions of such an investigation.
One viable research strategy to circumvent this problem is to explore perceptual disagreements instead. These are arguably sufficiently free of preconceptions – innocent enough – that people are open-minded to the outcomes of such research.
Fortuitously, we were blessed with the dress – an image that evokes vehement disagreement about perception.
However, this image – and others like it – were mostly considered but mere curiosities.
This is a fair point – until now, no one was able to intentionally create such displays, so it was unclear whether the disagreement about the colors of the dress has significance beyond the idiosyncratic quirkiness of that particular image, or if there are wider implications.
We derived a principle underlying the nature of disagreement, which allows us to design perceptually ambiguous displays at will, and – in turn – understand how disagreement comes about in general.
Let’s illustrate this general principle with a specific example, the case of color, and – even more specifically – a particular type of footwear, crocs. We first create uncertainty about the color of the crocs by removing any cues that would be present under typical viewing conditions. We then illuminate the crocs with colored lights so that they appear as some shade of grey. We finally add a second object that has a characteristic color – like a white tube sock – that reflects the color of the lighting, but which could be any color.
This – in turn – creates the disagreement. Some observers will take the appearance of the object at face value and perceive grey crocs, with colored socks. Others will remember that socks like that are usually white and use this subtle cue to calibrate the lighting of the overall display, perceiving pink crocs, as they would appear under normal lighting, and with white socks, see gif.
We call this principle SURFPAD (Substantial Uncertainty combined with Ramified or Forked Priors and Assumptions yields Disagreement). We used it to create several color ambiguous displays of crocs and surveyed a large number of observers about their perceptions.
We found that observers indeed disagree about the color of the crocs and that the way an individual observer perceives the crocs depends on how they interpret the socks. Observers who think the socks are white – despite them objectively appearing colored – are likely to see the crocs as if they were illuminated with natural light (pink), whereas those who see the socks as colored don’t. In turn, the propensity to see the socks as white in the first place was linked to one’s experience with these socks. Finally, we show that the individual perception of the crocs has no bearing on how someone sees the dress, highlighting that croc perception involves a different kind of assumption – assumptions about fabrics, not assumptions about light, like in the dress. Put differently, this is not just a warmed over dress effect – it is superficially similar, but separate and novel.
There are several wider implications of this research. First, as you can see for yourself, the effect is stronger if you focus on the red dot – or on a part of the socks instead of the crocs. This could reflect the fact that the color signal coming from photoreceptors is stronger in the fovea (where there are more cones) than in the periphery. Of course, if you already perceive the crocs as grey even if they are illuminated with green light, they should not change color subjectively.
This brings us to some of the more psychological possibilities one could consider. For instance, most people think they see things how they really are. However, in this case, that presents a conundrum: When presenting displays created with SURFPAD principles to observers, we found that whereas some saw the crocs like the pixels as they really appear on their monitors – grey – others saw the crocs as pink – the color they really are as the manufacturer intended them to appear when viewed under everyday lighting conditions. So does “really” mean “grey”, as an analysis of the pixels with photoshop would yield or does “really” mean “pink”, the color that the manufacturer intended to sell? Related to this is the question of whether someone sees objects in terms of their isolated component elements – the grey pixels – or the colored crocs as wholes in the context of particular lighting. Moreover, this could touch on another personality difference, namely whether someone (perceptually) “lives in the past” – by taking information from prior experience into account more strongly than those who don’t.
What all of these considerations have in common is that they require further research – these tendencies could reflect general personality characteristics, but it is also possible that these individual effects do not transfer to other displays.
As it is, this research does suggest that perception and cognition are more closely intertwined than previously believed, as one’s beliefs can demonstrably color perception. That is important because if cognition plays a large role in perception, it is plausible that perceptual principles in turn underlie cognitive phenomena. Our findings open up a new avenue of research – instead of studying cognition in a siloed fashion (i.e. studying memory completely independently from studying other cognitive functions like attention or perception), as has been the norm, we can now attempt to use perception as a bridgehead to gain traction on more elusive cognitive phenomena.
For instance, it is clear cultural effects play a large role in shaping the human experience. However, culture is extremely hard to study. In contrast, studying culture on a perceptual footing – as a set of shared experiences and assumptions – is much more tractable. Imagine a culture where people wear one kind of garment – say white socks and another culture where they wear black socks. We now have clear predictions as to what people from these cultures would perceive if they were confronted with displays engineered with SURFPAD principles.
But the real value of this principle might lie in a deeper understanding of disagreement about more controversial topics. While we need to study this directly, it is quite conceivable that the same principles that govern perceptual are those that underlie conceptual disagreement. It has been the source of considerable uneasiness that people with unorthodox but dearly held beliefs that are central to their identity (such as anti-vaxxers or flat-earthers) are essentially immune to being convinced of alternative views. Introducing challenging evidence does not change their beliefs. If anything, it strengthens them. This might appear puzzling, but makes complete sense in a SURFPAD framework. Consider the following hypothetical. Imagine that every day, newspapers write an article pointing out that a certain politician is a bad person. Naively, one could think that if the media is doing that, they will paint the figurative socks as really, really green, and readers should be swayed and start to realize that the politician in question is indeed a bad person. And this would work, if people had no preconceptions. But they do. For instance, some people know that the socks are actually white. For those people, seeing really green socks will make them conclude that the lighting is off and just allow them to estimate better just how off it is. And people will have no problem believing that, as they know that anyone can be put in a bad light, and levels of trust in the media are rather low, so people are quite ready to believe that the media would alter the lighting.
Note that in this model, no updating of the prior beliefs takes place, even with repeated exposure, as the socks are still seen as white, the crocs still as colored and the lighting is still discounted, in a cascade of polarized interpretations. If anything, the belief in the color of the socks and the biased light is strengthened.
So what is one to do if one wants to change someone’s mind, particularly about dearly held beliefs?
Our research suggests that simply presenting new evidence is not going to be compelling, as it will be interpreted in light of the pre-existing framework of assumptions. Instead, there are two potentially effective avenues for changing someone’s mind. First, highlighting assumptions directly and questioning why they are made in the first place promises some success. Second, one could address the potential for confusion between sock and light color directly – and offer a more compelling alternative scenario, i.e. pointing out why in this particular situation, it is more likely that the socks are actually green, and that the lighting is still white. Third, maybe we should incentivize a culture that discourages – not encourages – the ramification of priors.
To summarize, it is clear why the brain has to make these assumptions in order to operate effectively in an uncertain world. The necessary information to act is not always available, so it is prudent to make educated guesses. Under normal conditions, this works reasonably well, which is why we are all still here. However, what is nefarious about this is that your brain does not tell you when it quietly jumps to – unwarranted – conclusions by over-applying assumptions, much like autocorrect is often largely aspirational – it isn’t actually correct all that often.
In the area of politics, this is dangerous, as different people will apply different sets of assumptions (or priors), and there are now entire industries dedicated to the ramification of these priors. We have to come to terms with the ongoing and intentional forking and ramification of priors and its deleterious impact on civil discourse in one way or the other if we are to avoid the downside of this process. Given uncertainty and forked priors, disagreement might be inevitable, yet conflict might be avoidable. We suggest to achieve this by bringing about a new culture of disagreement on the basis of SURFPAD principles.
If you want to contribute to a follow-up of this research, you can do so here.
In order to learn from history, one has to know about it first. Even then, it is hard to do – arguably, human nature is constant, but how it manifests is ever changing, as the circumstances change, mostly due to innovation, which has led some to observe that history rhymes more so than it repeats, which is also hard to assess, as there is only one human history, in other words observing counterfactuals is impossible – there is neither a control group, nor the possibility of experiments. All of which makes “lessons from history” far more ambiguous than one would like.
But I rather seriously digress, and in the very first paragraph, no less. Back to the question, which could be phrased as “How aware are we of things that happened before we were born?, “How well will things that are popular today be remembered in the future?”, “How fleeting is fame and what determines which ideas will stand the test of time?”
Anecdotally, the answer to the first questions is “not very”. Every year, Beloit College publishes an updated “Mindset List” that attempts to highlight all the things that students who are now entering college are completely unaware of, as they have never used a typewriter, floppy disks, don’t know about VHS or cassette tapes, and so on. While amusing, such considerations raise deeper scientific questions: How well do cultural artifacts age in the collective memory? Will future generations have any awareness of things that are popular today?
Of course, there is longstanding interest in the question of what is in the cultural awareness, as exemplified by wild but popular speculations about archetypes, but scientific answers have been wanting until relatively recently.
One such investigation pertains to American presidents and Chinese leaders, both picked because the list of entries is comprehensive and known. In brief, the results show that collective memory mirrors individual memory – there are strong primacy and recency effects. In terms of American presidents, this manifests as knowing the first few and the most recent view, but most people would be hard pressed to name an American president from the middle of the 19th century other than Lincoln.
This paints a rather depressing picture of cultural transmission. As time progresses, most events will be “somewhere in the middle”, so are we doomed to live the cultural version of Eternal Sunshine of the Spotless Mind, with relatively little transmission between generations?
A somewhat more positive picture emerges when considering cultural artifacts that people seek out, e.g. music. Looking at onetime number 1 hits, we could show that recognition of these songs does not hit zero about a decade before our participants were born – what one would get if one extrapolated the steep drop-off implied by the recency effect.
Instead, recognition hits a rather stable “plateau” of moderate recognition that extends for 3 decades. Averaging is somewhat misleading, as there is tremendous inter-song variability in this period. Some are as well recognized as if they were released yesterday, whereas others are completely forgotten.
What drives this difference seems to be exposure, as measured by Spotify playcounts. In other words, we can’t tell whether music from the 60s to 90s was truly special, or whether recognition rates for things people seek out (music) are higher than for things people don’t (political leaders) in general.
The good news is that cultural transmission seems to work better than previously thought, at least for things that people are seeking out. Whether music is a fluke or not in this regard could be investigated by looking at other things like popular movies or books.
Obviously, you can believe whatever you want about metaphysics, as there is no observable reality to constrain you. That said, I believe the usual debates about theism vs. atheism miss the point. The real issue is not whether the world was created by a god – with endless debates about who has the burden of proof… theists asserting that there is a god, or atheists that there is not, others discussing or disputing specific characteristics of this god. However, this already casts the issue in terms that are comprehensible to human understanding, and there is no a priori reason why we should presuppose that reality is amenable to that – what is really going on might be much more ineffable. Instead, I propose that the real issue is whether the world is meaningful or not. In other words, does existence have a purpose? I would say so – as it is awfully specific. My mind is linked to my brain, and not yours. Why is it today, right now? It is also profoundly strange – you just got used to it. What exactly did you wake up from, when you woke up this morning? And what happened to yesterday – where did the time go? And not everything about this reality is observable. For instance, mathematical objects (e.g. numbers) are not observable in principle, but mathematics has – Goedel nonwithstanding – excellent and rigorous methods to assess the truth status of mathematical statements. Also, why does the universe have a very specific content of mass and energy, and in its current mix/configuration? Why these forces, and not others? Everything about our reality seems to be quite specific. Why even have rules in the first place and where is the computational overhead of the universe that decides what happens next? What even does it mean to be “next”? Of course you could say that there is a larger – unobservable – multiverse that explains these things, but that is strictly speaking also a metaphysical (in principle unfalsifiable) statement about reality. In other words, the fundamental question is whether the world is meaningful or not. Here is where Pascal’s wager 2.0 comes in. It literally costs you nothing to assume that the universe is meaningful – or has a purpose – because you lose absolutely nothing if you are wrong. Because then, you are wrong but nothing matters anyway as everything is genuinely pointless. You can argue that this is just as cynically utilitarian and therefore without moral value as the original wager, but I don’t think you can argue its basic validity. So to summarize, there is no way to tell whether reality is meaningful or not, but you lose nothing by assuming it is. The catch is that it is probably impossible to ascertain the purpose of a system from within the system. Of course this state of affairs is so vexing that it points to there being a purpose – what kind of system could hold such conundrums for no reason at all? It would be a pitiful waste indeed.
This is – by the way – a good example of dialectics:
Level 0: Believe what people around you believe/your culture raised you to believe
Level 1: Pascal’s Wager – belief is not arbitrary – it is rational to believe in god, due to the asymmetric utility of outcomes. If you falsely believe that there is a god, you lose nothing, but if you are wrong about that, you lose a lot (by going to hell).
Level 2: That’s a fallacy because “belief in god” is not specific enough. Based on the wager, it would be rational to adopt (or create) a religion with beliefs that spell out the greatest discrepancy in outcomes between believers and nonbelievers in terms of the afterlife (ultimate rewards vs. ultimate punishment). It also raises the issue of moral desert, putting the moral value of someone’s actions in question – do even good actions have any moral value, if they are ultimately made for entirely selfish reasons?
Level 3: Pascal’s Wager 2.0 – it is rational to believe that reality/existence has a purpose/is meaningful because you really do not lose anything if it turns out that you are wrong. Because then, nothing matters anyway. In addition – from a purely utilitarian perspective – as suffering necessarily outweighs pleasure for the vast majority of beings in this plane of existence, having no meaning to make up for this deficit is truly a brutal way of life. Of course, sentient beings torturing each other forever might be the purpose of this place (it would certainly be consistent with a lot of the evidence), as there is no guarantee that the purpose is a good purpose. Just that it is not entirely meaningless.
The notion of “data types” is probably the most underrated concept outside of computer science that I can think of right now. Briefly, computers use “typed variables” to represent numbers internally. All numbers are internally represented as a collection of “binary digits” or “bits” (a concept introduced by the underrated genius John Tukey, who also gave us the LSD test and the fast Fourier transform, among other useful things), more commonly known to the general public as “zeroes and ones”. An electric switch can either be on (1) or off (0) – usually implemented by voltages that are either high or low. So as a computer ultimately represents all numbers as a collection of zeroes and ones, the question is how many of them are used. A set of 8 bits make up a “byte”, usually the smallest unit of memory. So with one byte of memory, we can represent 2^8 or 256 distinct states of switch positions, i.e. from 00000000 (all off) to |||||||| (all on), and everything in between. And that is what data types are building off of. For instance, an “integer” takes up one byte in memory, so we can represent 256 distinct states (usually numbers from 0 to 255) with an integer. Other data types such as “single precision” take up 32 bits (=4 bytes) and can represent over 4 billion states (2^32) whereas “double precision” that are represented by 64 bits (=8 bytes of memory) and that can represent even more states. In contrast, the smallest possible data type is a Boolean, which can technically be represented by a single bit and that can only represent two states (0 and 1), which is often used when checking conditionals (“if these conditions are true (=1), do this. If they are not true (or 0), do something else”).
Each switch by itself can represent 2 states, 0 (“false”, represented by voltage off) and 1 (“true”, represented by voltage on). Left column: This corresponds to the k in 2^k . Right column: This corresponds to the number of unique states that this set of binary switches can represent.
Note that all computer memory is finite (and used to be expensive), so memory economy is paramount. Do you really need to represent every pixel in an image as a double or can you get away with an integer? How many shades of grey can you distinguish anyway? If the answer is “probably less than 256”, then you can save 87.5% of memory by representing the pixel as an integer, compared to representing it as a double. If the answer is that you want to go for maximal contrast, and “black” vs. “white” are the only states you want to represent (no shades of grey), then booleans will do to represent your pixels.
But computer memory has gotten cheap and is getting ever cheaper, so why is this still an important consideration?
Because I’m starting to suspect that something similar is going on for cognition and cognitive economy in humans and other organisms. Life is complicated and I wonder how that complexity is represented in human memory. How much nuance does long term memory allow for? Phenomena like the Mandela effect might suggest that the answer is “not much”. Perhaps long term memory only allows for the most sparse, caricature-like representation of objects (“he was for it” or “he was against it”, “the policy was good” or “the policy was bad”). Maybe this is even a feature to avoid subtle nuance-drift over time and keep the representation relatively stable over time, once encoded in long term memory.
But the issue doesn’t seem to be restricted to long term memory. On the contrary. There is a certain simplicity that really doesn’t seem suitable to represent the complexity of reality in all of its nuances, not even close, but people seem to be drawn to it. In fact, often the dictum “the simpler the better” seems to have a particular draw. This goes for personality types (I am willing to bet that much of the popularity of the MBTI in the face of a shocking lack of reliability can be attributed to the fact that it promises to explain the complexity of human interactions with a mere 16 types – or a 4 bit representation), horoscopes (again, it would be nice to be able to predict anything meaningful about human behavior with a mere 12 zodiac signs (3.5 bit (if bit were non-integers))), racism (maybe there are 4-8 major races, and thus can be represented with 2-3 bits), and sexism (biological sex used to be conventionally represented with a single bit). There is now even a 2-bit representation of personality that is rapidly gaining popularity – one that is based on the 4 blood types, and that has no validity whatsoever. But this kind of simplicity is hard to beat. In other words, all of these are “low memory plays”. If there is even a modicum of understanding about the world to be gained from such a low memory representation (perhaps even well within the realms of “purely felt effectiveness”, from the perspective of the individual, given the effects of confirmation bias, etc.), it should appeal to people in general, and to those who are memory-limited in particular.
Given this account, what remains puzzling – however – is that this kind of almost deliberate lack-of-nuance is even celebrated by those who should know better, i.e. people who are educated and smart enough that they don’t *have to* compromise and represent the world in this way, yet seem to do it anyway: For instance, there are some types of research where preregistration makes a lot of sense. If only to finally close the file drawer. Medication development comes to mind. But there are also some types where it makes less sense and some types where it makes no sense (e.g. creative research on newly emerging topics at the cutting edge of science) – so how appropriate it actually is mostly depends on your research. Surely, it must be possible for sophisticated people to keep a more nuanced position than a purely binary one (“preregistration good, no preregistration bad”) in their head. This goes for other somewhat sophisticated positions where tribalism rules the roost, e.g. “R good, SPSS bad” (reality: This depends entirely on your skill level) or “Python good, Matlab bad” (reality: Depends on what you want – and can – do) or “p-values bad, Bayes good” (reality: Depends on how much data you have and how good your priors are). And so on…
Part of the reason these dichotomies for otherwise sophisticated topics are so popular must then lie in the fact that such a low-memory, low-nuance representation – after all, it even takes 6 bits to represent a mere 49 shades of grey and 49 shades isn’t really all that much – has other hidden benefits. One is perhaps that it optimally preserves action potential (no course of action is easier to adjudicate than a binary choice – you don’t need to be an octopus to represent these 2 options) and it engenders tribalism and group cohesion (assuming for the sake of argument that this is actually a good thing). A boolean representation has more action potential and is more conducive to tribalism than a complex and nuanced one, so that’s perhaps what most people instinctively stick with…
But – and I think that is often forgotten in all of this – action potential and group cohesion nonwithstanding, there are hidden benefits to be able to represent a complex world in sufficient nuance as well. Choosing a data type that is too coarse might end up representing a worldview that is plagued by undersampling and suffers from aliasing. In other words, you might be able to act fast and decisively, but end up doing the wrong thing because you picked from two alternatives that were not without alternative – you fell prey to a false dichotomy. If a lot is at stake, this could matter tremendously.
In other words, even the cognitive utility of booleans and other low memory data types is not clear cut – sometimes they are adequate, and sometimes they are not. Which is another win for nuanced datatypes. Ironically? Because if they are superior, maybe it is a binary choice after all. Or not. Depending on the dimensionality of the space one is evaluating all of this in. And whether it is stationary. And so on.
At this point, we’re all *well* beyond peak #Yannygate. There have been comprehensive takes, there have been fun ones and there have been somber and downright ominous ones. But there have not been short ones that account for what we know.
This is the one (minute read). Briefly, all vowels that you’ve ever heard have 3 “formant frequencies” – 3 bands of highest loudness in the low (F1: ~500 Hz), middle (F2: ~1500 Hz) and high (F3: ~2500 Hz) frequency range. These bands are usually clearly visible in any given “spectrogram” (think “ghosts”) of speech.
However, the LaurelYanny sound doesn’t have this signature characteristic of speech. The F2 is missing. But your brain has no (epistemic) modesty. Instead of saying: “I have literally never heard anything like this before, is this even speech?”, it says: “I know exactly what this is” and makes this available to your consciousness as what you hear, without telling you that this is a guess (might be worth mentioning that, no)?
Stylized version of the Laurel and Yanny situation: Diagram of spectrograms. “Laurel” has all 3 formants, but with most power in the low frequencies. “Yanny” has all 3 formants, but with most power in the high frequencies. “LaurelYanny” has both high and low power, but nothing in the middle. So you have to guess.
That’s pretty much it. The signal contains parts of both “Laurel” and “Yanny”, but also misses parts of both, hence the need to guess. WHAT you are guessing and why you hear “Laurel”, “Yanny” or sometimes one, then the other, and what it means for you whether you are a “Laurel” or a “Yanny” is pretty much still open to research.
Action potential: Hopefully, that was a mercifully short read. If you have some more time – specifically another 7-9 minutes – and want to help, click here.
Technological change often entails social change. Historically, many of these changes were unintended and could not be foreseen at the time of making the technological advances. For instance, the printing press was invented by Johannes Gutenberg in the 1400s. One can make the argument that this advance led to the reformation within a little more than 50 years and the devastating 30-years war within another 100 years of that. Arguably, the 30-years war was an attempt at the violent resolution of fundamental disagreements – about how to interpret the word of god (the bible), which had suddenly become available for the masses to read. Of course the printing press was probably not sufficient to bring these developments about, but one can make a convincing argument that it was necessary. Millions of people died and the political landscape of central Europe was never quite the same.
Which brings us to social media. I think it is safe to say that most of us were surprised how fundamentally we disagree with each other as to how to interpret current events. Previously, the tacit assumption was that we all kind of agree about what is going on. This is obviously no longer possible and often quite awkward. Social media got started in earnest about 10 years ago, with the launch of Twitter and the Facebook News Feed. Since then, people have shared innumerable items on social media and from personal experience, one can be quite surprised how different other people interpret the very same event.
Which brings us to my research.
Briefly, people can fundamentally disagree about the merits of any given movie or piece of music, even though they saw the same film or listened to the same clip.
Moreover, they can vehemently disagree about the color of a whole wardrobe of things: Dresses, jackets, flipflops and sneakers. Importantly, nothing anyone can say would change anyone else’s mind in case of disagreement and these disagreements are not due to being malicious, ignorant or color-blind.
So where do they come from? When ascertaining the color of any given object, the brain needs to take illumination into account, a phenomenon known as color-constancy. Insidiously, the brain is not telling us that this is happening, it simply makes the end-result of this process available to our conscious experience. The problem – and the disagreement – arises when different people make different assumptions about the illumination.
Why might they do that? Because people assume the kind of light that they usually see, and this will differ between people. For instance, people who get up and go to bed late will experience more artificial lighting than those who get up and go to bed early. It stands to reason that people assume to happen in the future what they have experienced in the past. Someone who has seen lots of horses but not a single unicorn might misperceive a unicorn as a horse, should they finally encounter one. This is what seems to be happening more generally: People who go to bed late do assume lighting to be artificial, compared to those who go to bed early.
In other words, prior experience does shape our assumptions, which shapes our conclusions (see diagram).
Conclusions can be anything that the brain makes available to our conscious experience – percepts, decisions, interpretation. Objects above dashed line are often not consciously considered when evaluating the conclusions. Some of them might not be consciously accessible. Note that this is not the only possible difference between individuals. Arguably, it might be that the brains are also different from the very beginning. That is probably true, but we know next to nothing about that. Note that differing assumptions are sufficient to bring about differences in conclusions in this framework. That doesn’t mean other factors couldn’t matter as well. Also note that we consider two individuals here. Once more than two are involved, the situation would be more complicated yet.
If this is true more generally, three fundamental conclusions are important to keep in mind, if one wants to manage disagreement positively:
1. There is no point in arguing about the outcomes – the conclusions. Nothing that can be said can be expected to change anyone’s mind. Nor is it about the evidence (what actually happened), as the interpretation of that is colored by the assumptions.
2. In order to find common ground, one would be well advised to consider – and question – the assumptions you and others make. Ideally, it would be good to trace someone’s life experience, which is almost certain to differ between people. Of course, this is almost impossible to do. Someone’s life experience is theirs and theirs alone. No one can know what it is like to be someone else. But pondering – and discussing – on this level is probably the way to go. Maybe trying to create common experiences would be a way to transcend the disagreement.
3. As life experiences are radically idiosyncratic, fundamental and radical disagreements should be expected, frequently. The question is how this disagreement is managed. If it is not managed well, history suggests that bad things might be in store for us.
I understand the need of journalists to simplify quotes and make them more palatable to their audience. Academics have a tendency to hedge every statement. In fact, they would have to be an octopus to account for all the hands involved in a typical statement. From this perspective, it is fair that journalists would try to counteract this kind of nuance that their audience won’t appreciate anyway. However, I’m in the habit of choosing my words carefully and try to make the strongest possible statement that can be justified based on the available evidence. If journalists then apply their own biases, the resulting statements can veer into the ridiculous. So I’m now quoted – all over the place – saying the damnedest things, none of which I actually said. Sometimes, the quote is the opposite of what I said. This is not ok.
Of course you can write whatever you want. But that doesn’t include what I allegedly said. Note also that I did give journalists the benefit of the doubt in the past. But they demonstrably – for whatever reason, innocent or willful – did not care much for quote accuracy.
Thus – from now on, I must insist on quote review prior to publication. This is not negotiable, as my reputation is on the line and – again – I’m in the habit of speaking very carefully. This policy is also mutually beneficial – wouldn’t any journalist with integrity be concerned about getting the quotes right?
In the meantime, one should be wise to assume the media version of Miranda: “Everything you don’t say will be attributed to you anyway.”
It is happening again. Another “dress”-like image just surfaced.
As far as I can tell, more or less the same thing is going on. Ill defined lighting conditions in the images are being filled in by lighting assumptions, and they differ between people due to a variety of factors, including which light they have seen more of. Just as described in my original paper.
As we get better at constructing these (images with ill-defined illumination), I expect more of these to pop up periodically. But people now seem more comfortable (and less surprised) by the notion that we can see colors of the same image differently.
The reason these things are still a thing is our tacit assumption that we all more or less see the same reality as everyone else.
So if I’m right (which most people presume) and someone else disagrees, they have to be wrong, for whatever reason. Color stimuli like this seem to produce categorically and profoundly differing interpretations. Which is what makes them so unsettling.
I think the same thing – more or less – applies to social and political questions. We take our experience at face value and fill the rest in with assumptions that are based on prior experience. As people’s experiences will differ, disagreements abound.
Which is why I find these stimuli so interesting and which is why I study them in my lab.
Hopefully, as these become more common, it will make people more comfortable with the notion that they can fundamentally – but sincerely – disagree with their fellow man.
Because people operate experientially. Here, they experience benign disagreement. In contrast to politics, where the disagreement is often no longer benign.
So this kind of thing could be therapeutic.
We could use it.
Usually, I publicly comment on our work once it is published, like here, here or here.
So I was quite surprised when I was approached by the Guardian to comment on an unpublished abstract. Neuroscientists typically present these as “work in progress” to their colleagues at the annual Meeting of the Society for Neuroscience, which is held in Washington DC in November, this year and at which our lab has 5 such abstracts. Go to this link if you want to read them.
Given these constraints, the Guardian did a good job at explaining this work to a broader audience, emphasizing its preliminary nature (we won’t even attempt to publish this unless we replicate it internally with a larger sample of participants and songs) as well as some ethical concerns inherent to work like this.
What becomes apparent on the basis of our preliminary work is that we can basically rule out the popular stereotype that people with psychopathic tendencies have a preference for classical music and that we *might* be able to predict these tendencies on the basis of combining data from *many* songs – individual songs won’t do, and neither will categories as broad as genre (or gender, race or SES). To confirm these patterns, we need much more data. That’s it.
What happened next is that a lot of outlets – for reasons that I’m still trying to piece together – made this about rap music and a strong link between a preference for rap music and psychopathic traits.
As far as I can tell, there is no such link, I have never asserted there to be one and I am unsure as to the evidentiary basis of such a link at this point.
It is worth pointing out that I actually did not say most of the things I’m quoted as saying on this topic, or at least not in the form they were presented.
So all of this is a lesson in media communications. Between scientists and the media, as well as between media and media, media and social media and social media and people (and all other combinations).
So it is basically a game of telephone: What we did. What the (original) media thinks we did. What the media that copies from the original media think we did. What social media thinks we did. What people understand we did. Apparently, all these links are “leaky” or rather unreliable. Worse, the leaks are probably systematic, accumulating systematic error (or bias) based on a cascade of differential filters (presumably, media filters by what they think will gain attention, whereas readers will filter by personal relevance and worldview).
Given that, the reaction of the final recipient (the reader) of this research was basically dominated by their prior beliefs (and who could blame them), dismissing this either as obviously flawed “junk science” or so obvious that it doesn’t even need to be stated, depending on whether the media-rendering of the findings clashed with or confirmed these prior beliefs.
Is publicizing necessarily equal to vulgarizing?
I still think the question of identifying psychopaths based on more than their self-report is important. I also still think that doing so by using metrics without obvious socially desirable answers like music taste is promising, e.g. given their lack of empathy, psychopaths could be taken by particularly lyrics or given their need for stimulation, particular rhythms or beats could resonate with them more than average. But working all that out will take a lot more – and nuanced – work.
And to those who have written me in concern, I can reassure you: No taxpayer money was spent on this – to date.
If you are interested in this, stay tuned.
Hopefully, this will clear up some confusions regarding vector projections onto basis vectors.
Via Matlab, powered by @pascallisch
The term for science – scientia (knowledge) is terrible. Science is not knowledge. It is simply not (just) a bunch of facts. The German term “Wissenschaft” is slightly better, as it implies a knowledge creation engine. Something that creates knowledge, emphasizing that this is a process (and the only valid one we have as far as I can tell) that generates knowledge. But that doesn’t quite capture it either. Science does not prove anything, nor create any knowledge per se. Science has been wrong many times, and will be wrong in the future. That’s the point. It is a process that detects – via falsification – when we were wrong. Which is extremely valuable. So a better term is in order. How about uncertainty reduction engine? But incertaemeíosikinitiras probably won’t catch on.
How about incertiosikini? Probably won’t catch on either.
There is a fundamental tension between how movie critics conceive of their role and how their reviews are utilized by the moviegoing public. Movie critics by and large see their job as educating the public as to what is a good movie and explaining what makes it good. In contrast, the public generally just wants a recommendation as to what they might like to watch. Given this fundamental mismatch, the results of our study that investigated the question whether movie critics are good predictors of individual movie liking should not be surprising.
First, we found that individual movie taste was radically idiosyncratic. The average correlation was only 0.26 – in other words, one would predict an a
verage disagreement of 1.25 stars, out of a rating scale from 0 to 4 stars – that’s a pretty strong disagreement (max RMSE possible is 1.7). Note that these are individuals who reported having seen *the same* movies.
Interestingly, whereas movie critics correlated more strongly with each other – at 0.39 – which had been reported previously, on average they are not significantly better than a randomly picked non-critic at predicting what a randomly picked person will like. This suggests that vaunted critics like the late Roger Ebert gain prominence not by the reliability of their predictions, but other factors such as the force of their writing.
What is the best way to get a good movie recommendation? In absence of all other information, information aggregators of non-critics such as the Internet Movie Database do well (r = 0.49), whereas aggregators of critics such as Rotten Tomatoes underperforms, relatively speaking (r = 0.33) – Rotten Tomatoes is better at predicting what a critic would like (r = 0.55), suggesting a fundamental disconnect between critics and non-critics.
Finally, as taste is so highly idiosyncratic, your best bet might be to find a “movie-twin” – someone who shares your taste, but has seen some movies that you have not. Alternatively, companies like Netflix are now employing a “taste cluster” approach, where each individual is assigned to the taste cluster their taste vector is closest to, and the predicted rating would be that of the cluster (as the cluster has presumably seen all movies, whereas individuals, even movie-twins will not). However, one cautionary note about this approach is that Netflix probably does not have the data it needs to pull this off, as ratings are provided in a self-selective fashion, i.e. over-weighing those that people feel most strongly about, potentially biasing the predictions.
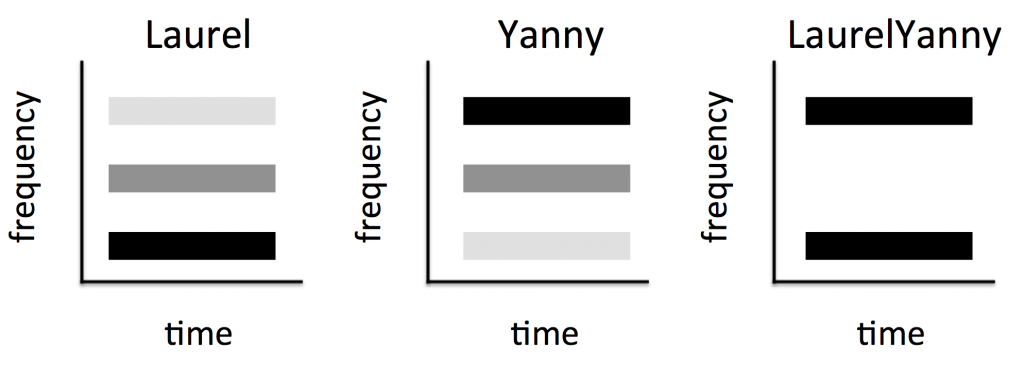
#Yannygate highlights the underrated benefits of keeping foxes around
In May 2018, a phenomenon surfaced that lends itself of differential interpretation – some people hear “Laurel” whereas others hear “Yanny” when listening to the same clip. As far as I’m concerned, this is a direct audio analogue of #thedress phenomenon that surfaced in February 2015, but in the auditory domain. Illusions have been studied by scientists for well over a hundred years and philosophers have wondered about them for thousands of years. Yet, this kind of phenomenon is new and interesting, because it opens the issue of differential illusions – illusions that are not strictly bistable, like Rubin’s vase or the Duckrabbit, but that are perceived as a function of the prior experience of an organism. As such, they are very important because it has long been hypothesized that priors (in the form of expectations) play a key role in cognition, and now we have a new tool to study their impact on cognitive computations.
What worries me is that this analogy and the associated implications were lost on a lot of people. Linguists and speech scientists were quick to analyze the spectral (as in ghosts) properties of this signal – and they were quite right with their analysis – but also seemed to miss the bigger picture, as far as I’m concerned, namely the directly analogy to the #dress situation mentioned above and the deeper implication of existence of differential illusions. The reason for that is – I think – that Isaiah Berlin was right when he stated:
“The fox knows many things, but the hedgehog knows one big thing.”
The point of this classification is that there are two cognitive styles by which different people approach a problem: Some focus on one issue in depth, others connect the dots between many different issues.
What he didn’t say is that there is a vast numerical discrepancy between these cognitive styles, at least in academia. Put bluntly, hedgehogs thrive in the current academic climate whereas foxes have been brought to the very brink of extinction.
Isiah Berlin was right about the two types of people. But he was wrong about the relative quantities. It is not a one-to-one ratio. So it shouldn’t be ‘the hedgehog and the fox’, it should be ‘the fox and the hedgehogs’, at least by now…
It is easy to see why. Most scientists start out by studying one type of problem. In the brain – owed to the fact that neuroscience is methods driven and it is really hard to master any given method (you basically have to be MacGyver to get *any* usable data whatsoever) – this usually manifests as studying one modality such as ‘vision’, ‘hearing’ or ‘smell’ or one cognitive function such as ‘memory’ or ‘motor control’. Once one starts like that, it is easy to see how one could get locked in: Science is a social endeavor, and it is much easier to stick with one’s tribe, in particular when one already knows everyone in a particular field, but no one in any other field. Apart from the social benefits, this has clear advantages for one’s career. If I am looking for a collaborator, and I know who is who in a given field, I can avoid the flakes and those who are too mean to make it worthwhile to collaborate and seek out those who are decent and good people. It is not always obvious from the published record what differentiates them, but it makes a difference in practice, so knowing one’s colleagues socially comes with lots of clear blessings. In addition, literatures tend to cite each other, silo-style, so once one starts reading the literature of a given field, it is very hard to break out and do this for another field: People tend to use jargon that one picks up over time, but that is rarely explicitly spelled out anywhere. People have a lot of tacit knowledge (also picked up over time, usually in grad school) that they *don’t* put in papers, so reading alien literatures is often a strange and trying experience, especially when compared with the comforts of having a commanding grasp on a given literature where one already knows all of the relevant papers. Many other mechanisms are also geared towards further fostering hedgehogs: One of them is “peer-review”, which must be nice because it is de facto review by hedgehog, which can end quite badly for the fox. Just recently, a program officer told me that my grant application was not funded because the hedgehog panel of reviewers simply did not find it credible that one person could study so many seemingly disparate questions at once. Speaking of funding: Funding agencies are often structured along the lines of a particular problem, for instance in the US, there is no National Institute of Health – there are the National Institutes of Health, and that subtle plural “s” makes all the difference, because each institute funds projects that are compatible with their mission specifically. For instance, the NEI (the National Eye Institute) funds much of vision research with the underlying goal of curing blindness and eye diseases in general. But also quite specifically. And that’s fine, but what if the answer to that question relies on knowledge from associated, but separate fields (other than the eye or visual cortex). More on this later, but a brief analogy might suffice to illustrate the problem for now: Can you truly and fully understand a Romance language – say French – without having studied Latin? Even cognition itself seems to be biased in favor of hedgehogs: Most people can attend to only one thing at a time, and can associate an entity with only one thing. Scientists who are known for one thing seem to have the biggest legacy, whereas those with many – often somewhat smaller – disparate contributions seem to get forgotten at a faster rate. In terms of a lasting legacy, it is better to be known for one big thing, e.g. mere exposure, cognitive dissonance, obedience or the ill-conceived and ill-named Stanford Prison Experiment. This is why I think all of Google’s many notorious forrays to branch out into other fields have ultimately failed. People so strongly associate it with “search”, specifically that their – many – other ventures just never really catch on, at least not when competing with hedgehogs in those domains, who allocate 100% of their resources to that thing, e.g. FB (close online social connections – connecting with people you know offline, but online) eviscerated G+ in terms of social connections. Even struggling Twitter (loose online social connections – connecting with people online that you do not know offline) managed to pull ahead (albeit with an assist by Trump himself), and there was simply no cognitive space left for a 3rd, undifferentiated social network that is *already* strongly associated with search. LinkedIn is not a valid counterexample, as it isn’t as much a social network, as it formalized informal professional connections and put them online, so it is competing in a different space.
So the playing field is far from level. It is arguably tilted in the favor of hedgehogs, has been tilted by hedgehogs and is in danger of driving foxes to complete extinction. The hedgehog to fox ratio is already quite high in academia – what if foxes go extinct and the hedgehog singularity hits? The irony is that – if they were to recognize each others strengths – foxes and hedgehogs are a match made in heaven. It might even be ok for hedgehogs to outnumber foxes. A fox doesn’t really need another fox to figure stuff out. What the fox needs is solid information dug up by hedgehogs (who are admittedly able to go deeper), so foxes and hedgehogs are natural collaborators. As usual, cognitive diversity is extremely useful and it is important to get this mix right. Maybe foxes are inherently rare. In which case it is even more important to foster, encourage and nurture them. Instead, the anti-fox bias is further reinforced by hyper-specific professional societies that have hyper-focused annual meetings, e.g. VSS (the vision sciences society) puts on an annual meeting that is basically only attended by vision scientists. It’s like a family gathering, if you consider vision science your family. Focus is important and has many benefits – as anyone suffering from ADD will be (un)happy to attest, but this can be a bit tribal. It gets worse – as there are now so many hedgehogs and so few remaining foxes, most people just assume that everyone is a hedgehog. At NYU’s Department of Psychology (where I work), every faculty member is asked to state the research question they are interested in, on the faculty profile page (the implicit presumption is of course that everyone only has exactly 1, which is of course true for hedgehogs and works for them. But what is the fox supposed to say? Even colloquially, scientists often ask each other “So, what do you study”, implicitly expecting a one-word answer like “vision” or “memory”. Again, what is the fox supposed to say here? Arguably, this is the wrong question entirely, and not a very fox-friendly one at that). This scorn for the fox is not limited to academia; there are all kinds of sayings that are meant to denigrate the fox as a “Jack of all trades, master of none” (“Hansdampf in allen Gassen”, in German), it is common to call them “dilettantes” and it is of course clear that a fox will appear to lead a bizarre – startling and even disorienting – lifestyle, from the perspective of the hedgehog. And there *are* inherent dangers of spreading oneself too thin. There are plenty of people who dabble in all kinds of things, always talking a good game, but never actually getting anything done. But these people give just give real foxes a bad name. There *are* effective foxes, and once stuff like #Yannygate hits we need them to see the bigger picture. Who else would? Note that this is not in turn meant to denigrate hedgehogs. This is not an anti-hedgehog post. Some of my closest friends are hedgehogs, and some are even nice people (yes that last part is written in jest, come on, lighten up). No one questions the value of experts. We definitely need people with a lot of domain knowledge to go beyond the surface level on any phenomenon. But whereas no one questions the value of keeping hedgehogs around, I want to make a case for keeping foxes around, too – even valuing them.
What I’m calling for specifically, is to re-evaluate the implicit or explicit “foxes not welcome here” attitude that currently prevails in academia. Perhaps unsurprisingly, this attitude is a particular problem when studying the brain. While lots of people talk a good game about “interdisciplinary research”, few people are actually doing it and even less are doing it well. The reason this is a particular problem when studying the brain is that complex cognitive phenomena might cut across discipline boundaries, but in ways that were unknown when the map of the fields was drawn. To make an analogy: Say you want to know where exactly a river originates – where its headwaters or source are. To find that out, you have to go wherever the river leads you. That might be hard enough, just like when Theodore Roosevelt did this with the River of Doubt, arguably all phenomena in the brain are a “river of doubt” in their own right, with lots of waterfalls and rapids and other challenges to progress. We don’t need artificial discipline or field boundaries to hinder us even further. We have to be able to go wherever the river leads us, even if that is outside of our comfort zone or outside of artificial discipline boundaries. If you really want to know where the headwaters of a river are, you simply *have to* go where the river leads you. If that is your primary goal, all other considerations are secondary. If we consider the suffering imposed by an incomplete understanding of the brain, reaching the primary objective is arguably quite important.
To mix metaphors just a bit (the point is worth making), we know from history that artificially imposed borders (without regard for the underlying terrain or culture) can cause serious problems long term problems, notably in Africa and the Middle East.
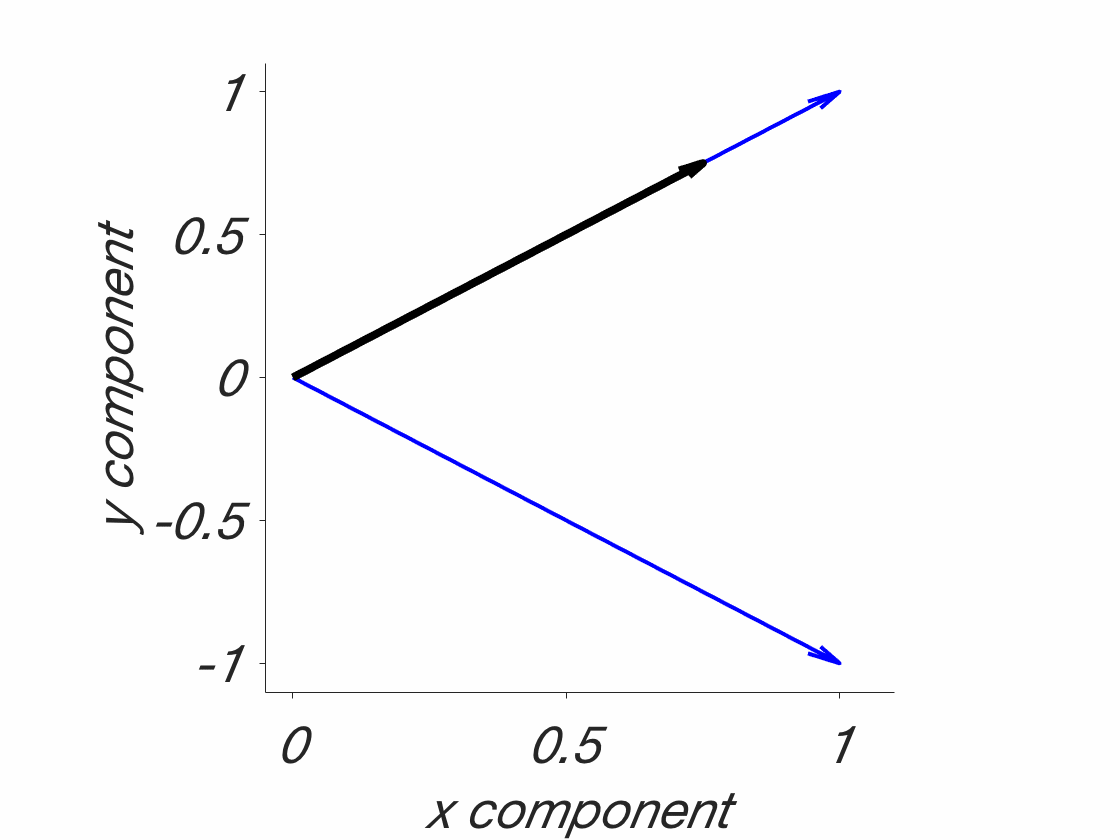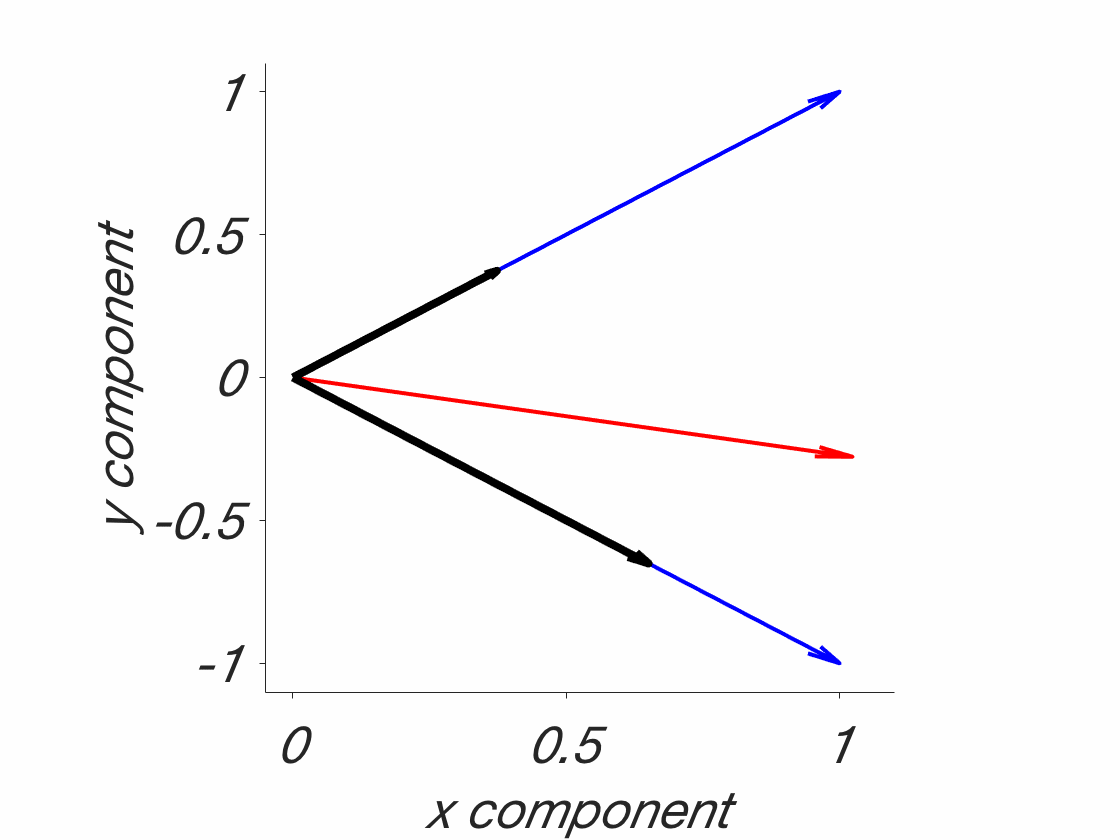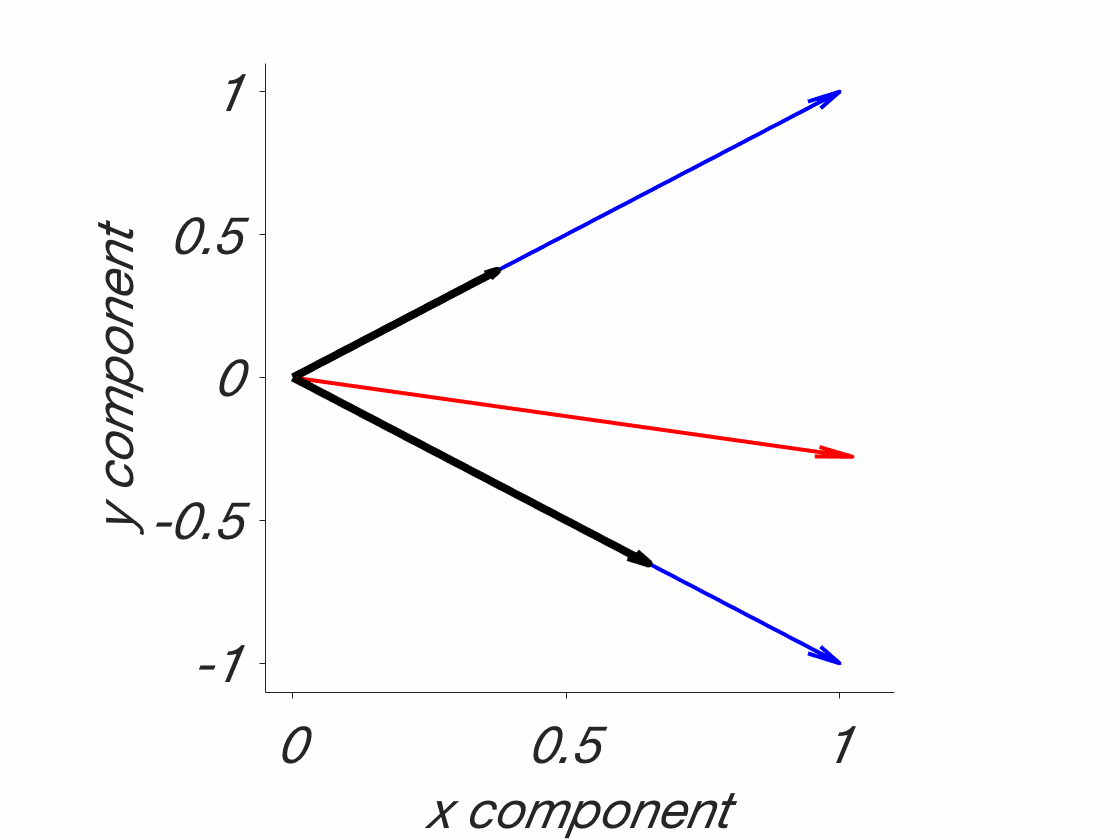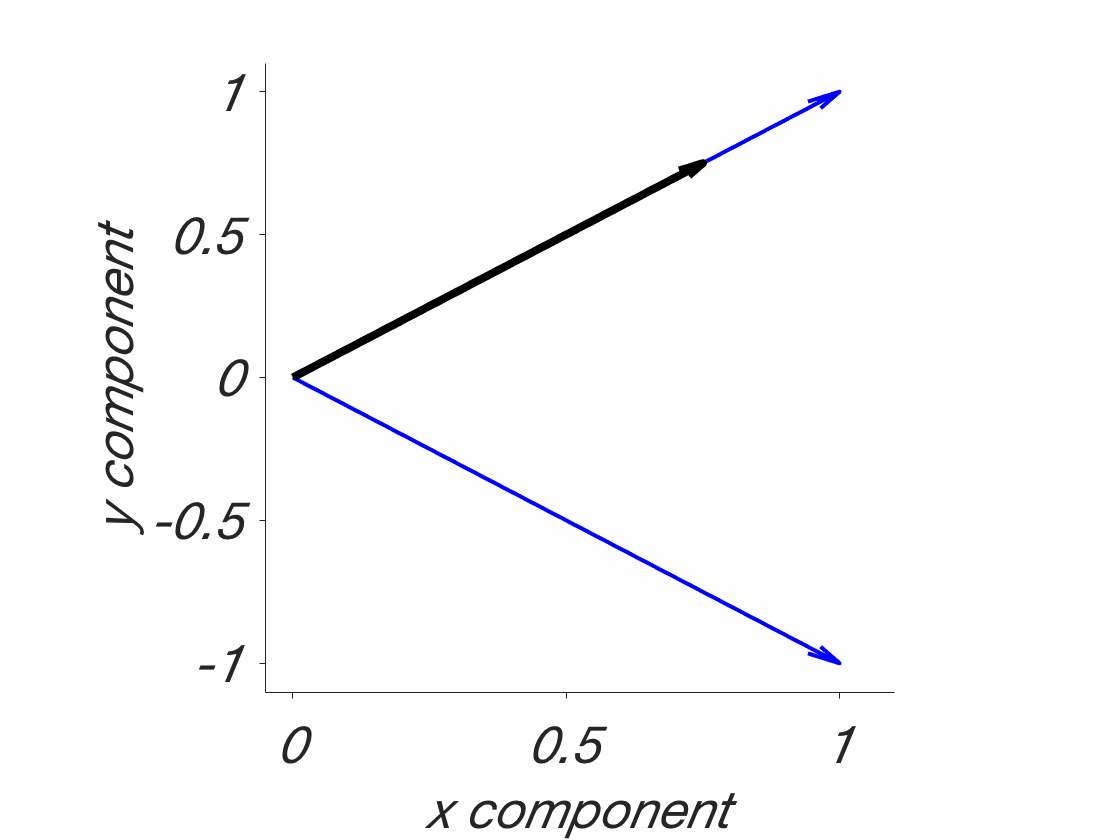
All of this boils down to an issue of premature tessellation:
The tessellation problem. Blue: Field boundaries as they should be, to fully understand the phenomena in question. Red: Field boundaries, as they might be, given that they were drawn before understanding the phenomena. This is a catch 22. Note that this is a simplified 2D solution. Real phenomena are probably multidimensional and might even be changing. In addition, they are probably jagged and there are more of them. This is a stylized/simplified version. The point is that the lines have to be drawn beforehand. What are the chances that they will end up on the blue lines, randomly? Probably not high. That’s why foxes are needed – because they transcend individual fields, which allows for a fuller understanding of these phenomena.
What if the way you conceived of the problem or phenomenon is not the way in which the brain structures it, when doing computations to solve cognitive challenges? The chance of a proper a priori conceptualization is probably low, given how complicated the brain is. This has bothered me personally since 2001, and other people have noticed this as well.
This piece is getting way too long, so we will end these considerations here.
To summarize briefly, being a hedgehog is prized in academia. But is it wise?
Can we do better? What could we do to encourage foxes to thrive, too? Short of creating “fox grants” or “fox prizes” that explicitly recognize the foxy contributions that (only) foxes can make, I don’t know what can be done to make academia a more friendly habitat for the foxes among us. Should we have a fox appreciation day? If you can think of something, write it in the comments?
Action potential: Of course, I expect no applause for this piece from the many hedgehogs among us. But if this resonates with you and you strongly self-identify as a fox, you could consider joining us on FB.